Fórmulas no Revit: Como utilizar as condicionais para aumentar a eficiência de Projeto
A revolução trazida pelo BIM nos seus mais diversos aspectos na construção civil está gradualmente transformando a indústria, com a finalidade de tornar os processos mais eficientes e assertivos tem como uma característica basilar a parametria.
Aplicado a modelagem de objetos e modelos esse conceito, quando usado de maneira equilibrada, automatiza processos repetitivos e garante a confiabilidade de informações.
O Revit, um dos principais e mais abrangentes softwares BIM, permite desenvolver combinações de fórmulas de níveis que vão da aritmética simples a operações de função avançadas, permitindo alcançar resultados impressionantes. Mas como e em que casos utilizar essas fórmulas? Esse artigo tem como objetivo demonstrar o uso da ferramenta neste aspecto.
A capacidade de personalizar e automatizar tarefas se torna cada vez mais um diferencial competitivo, visto que as fórmulas condicionais oferecem flexibilidade para que os profissionais possam adaptar o modelo conforme as necessidades de cada situação, sejam elas relacionadas ao dimensionamento de elementos, em configurações de materiais ou até mesmo à criação de componentes paramétricos inteligentes. Ao usar essas fórmulas, é possível não apenas acelerar o processo de dominar o projeto, mas também garantir uma maior solução nas soluções propostas.

OPERAÇÕES ARITMÉTICAS
As operações aritméticas são os cálculos básicos da matemática, que relacionam os algoritmos da maneira mais simples. Adição, subtração, multiplicação, divisão e exponenciação, através dela é possível realizar operações no Revit, através das seguintes regras:
- As operações podem ser feitas relacionando parâmetros e/ou números utilizando os símbolos de operação;
- Os parâmetros relacionados devem ser do tipo ‘número’ para o funcionamento da operação.
Tabela de Operações Aritméticas

DECLARAÇÃO CONDICIONAL
A declaração condicional é uma instrução em que permite executar uma atividade seguindo a regra de determinada condição. Dividindo o resultado em verdadeiro ou falso, assim os resultados promovem caminhos objetivos para os elementos programados.

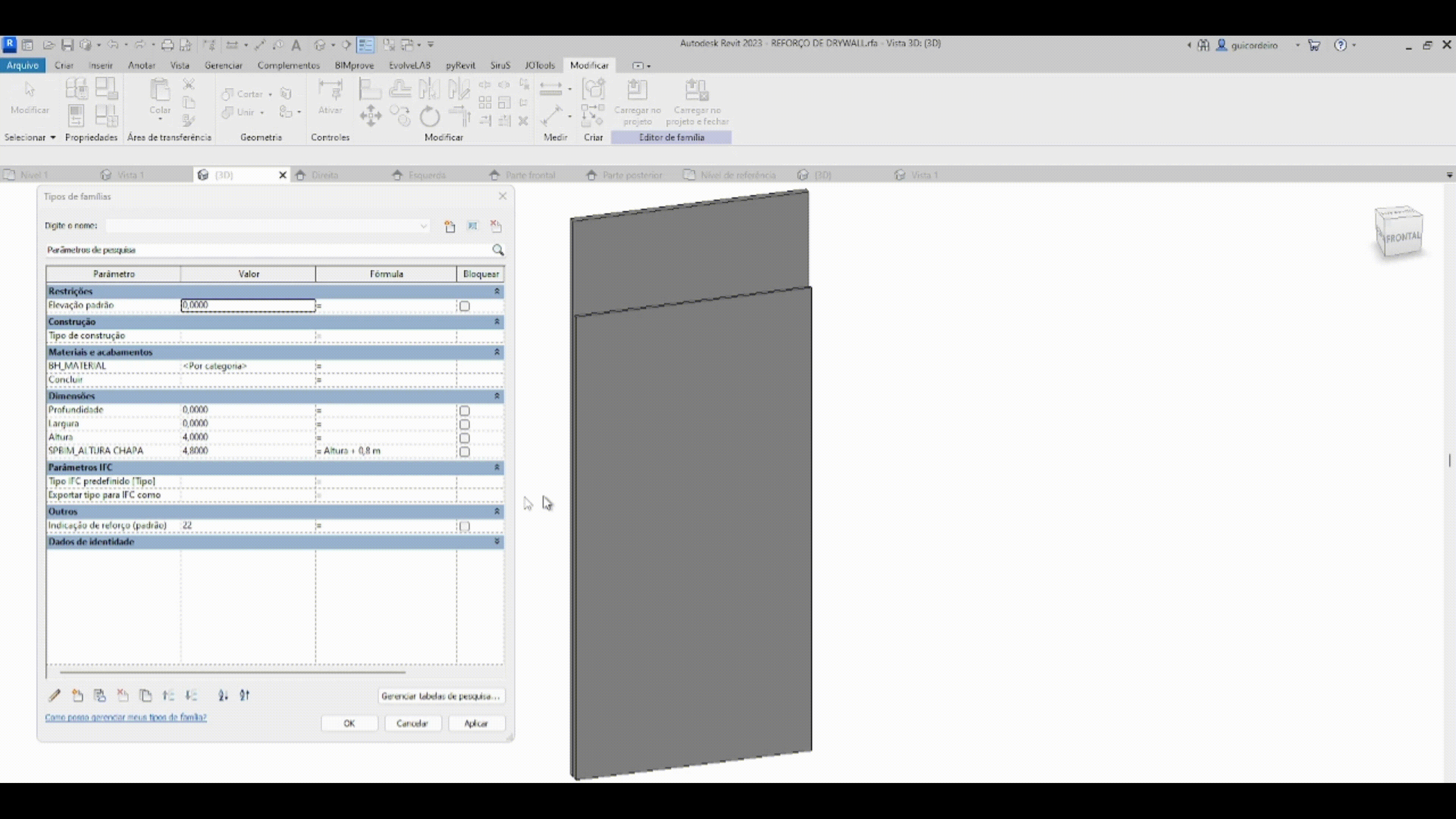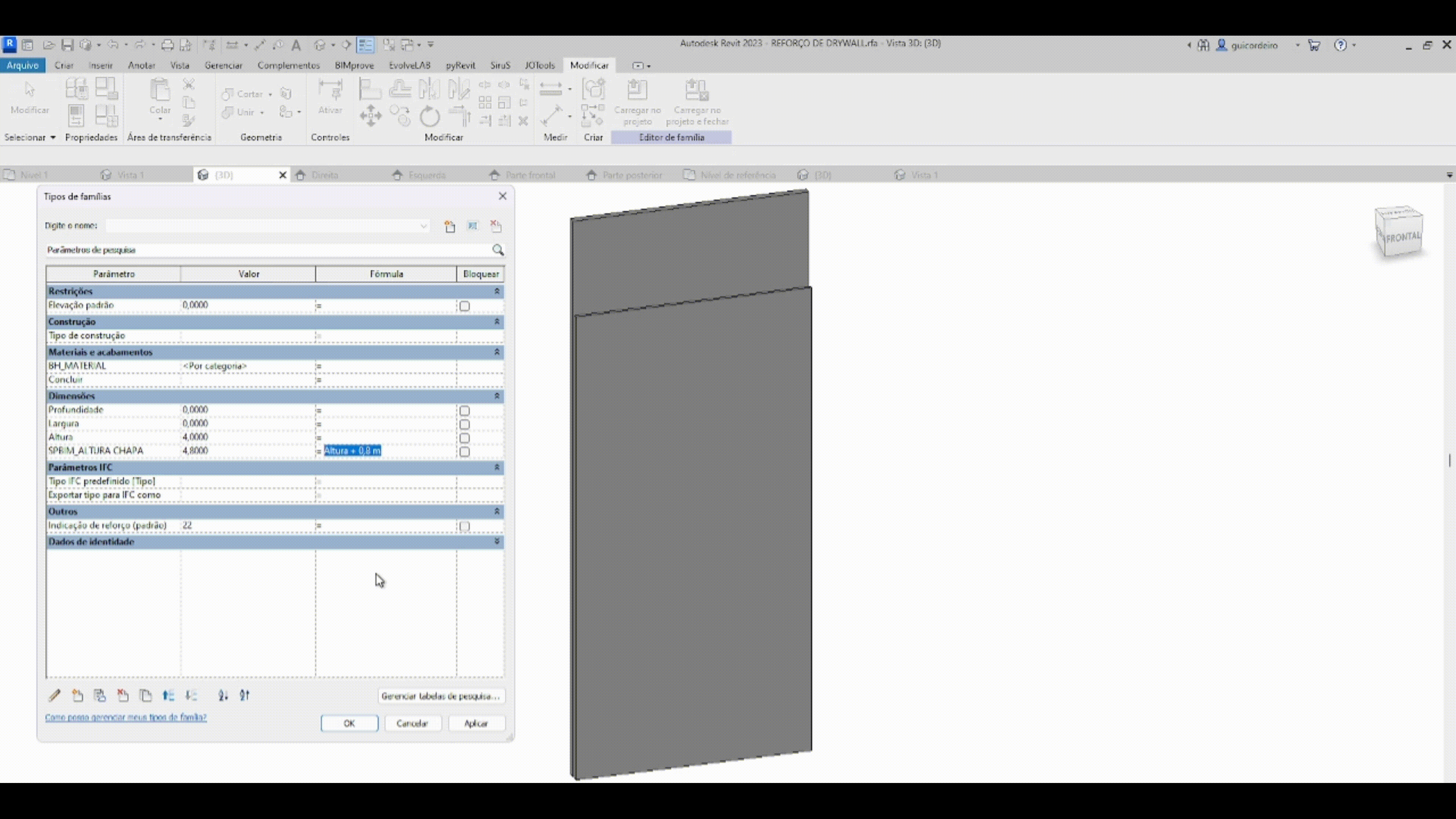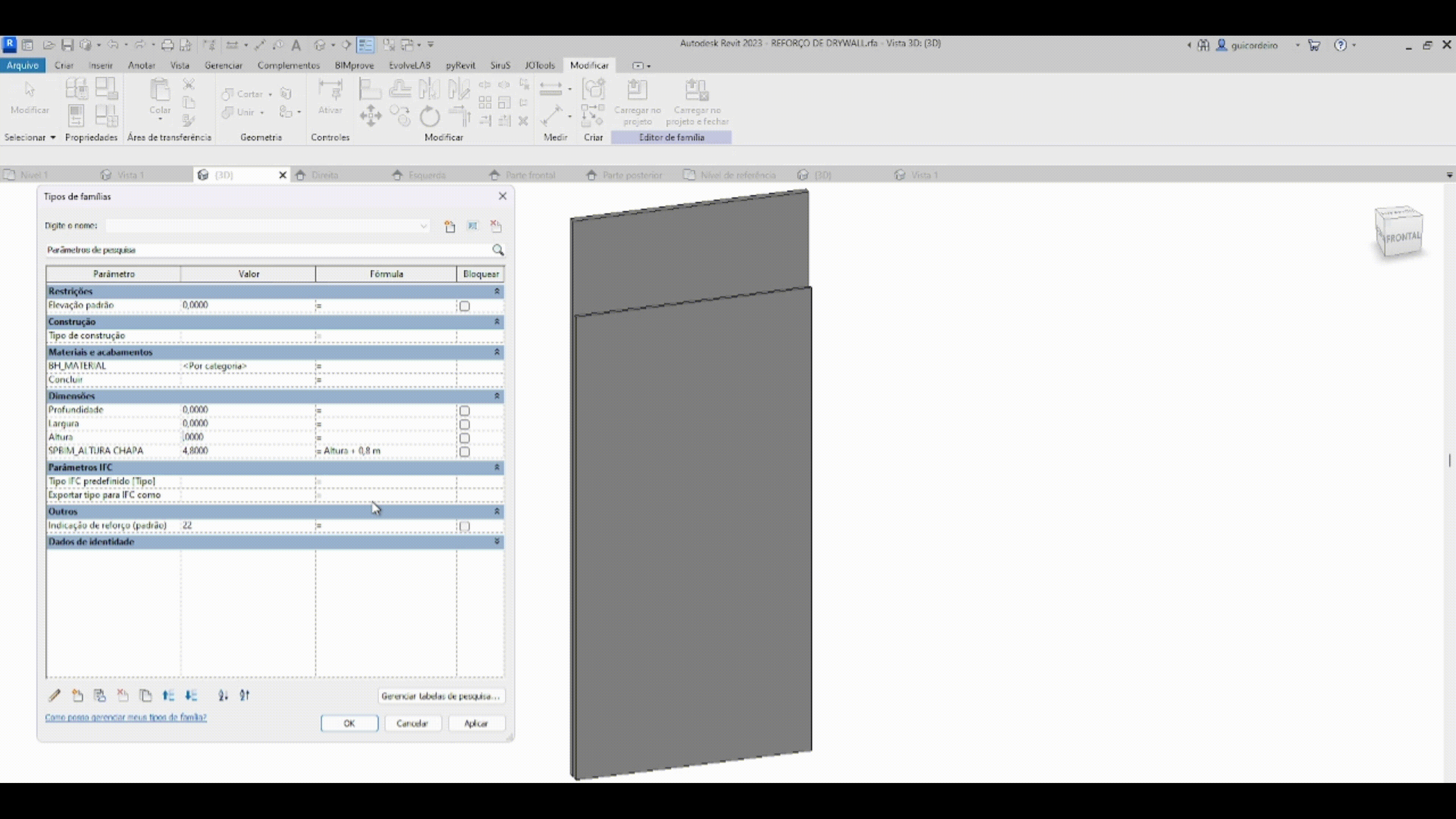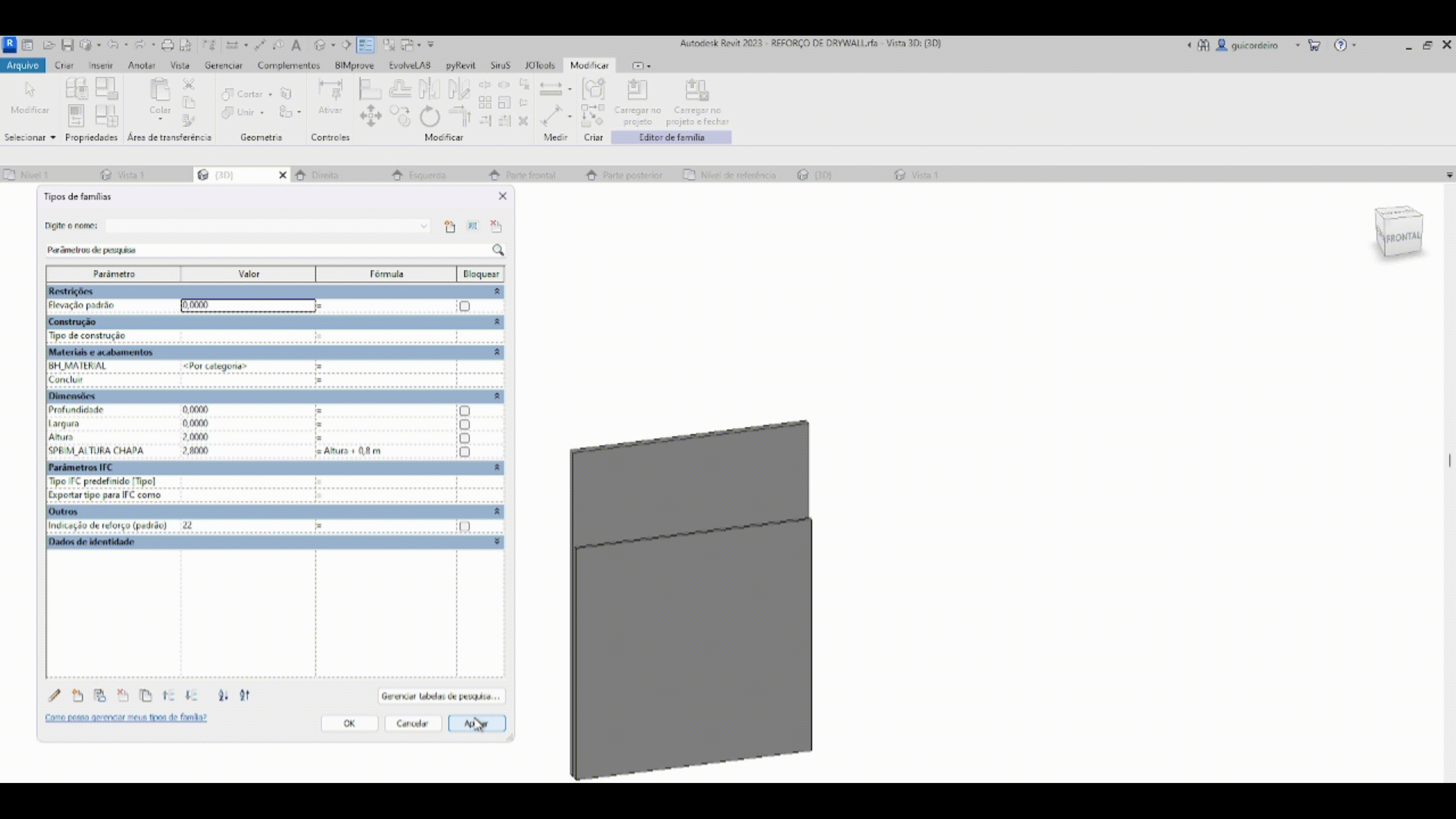
FÓRMULA CONDICIONAL
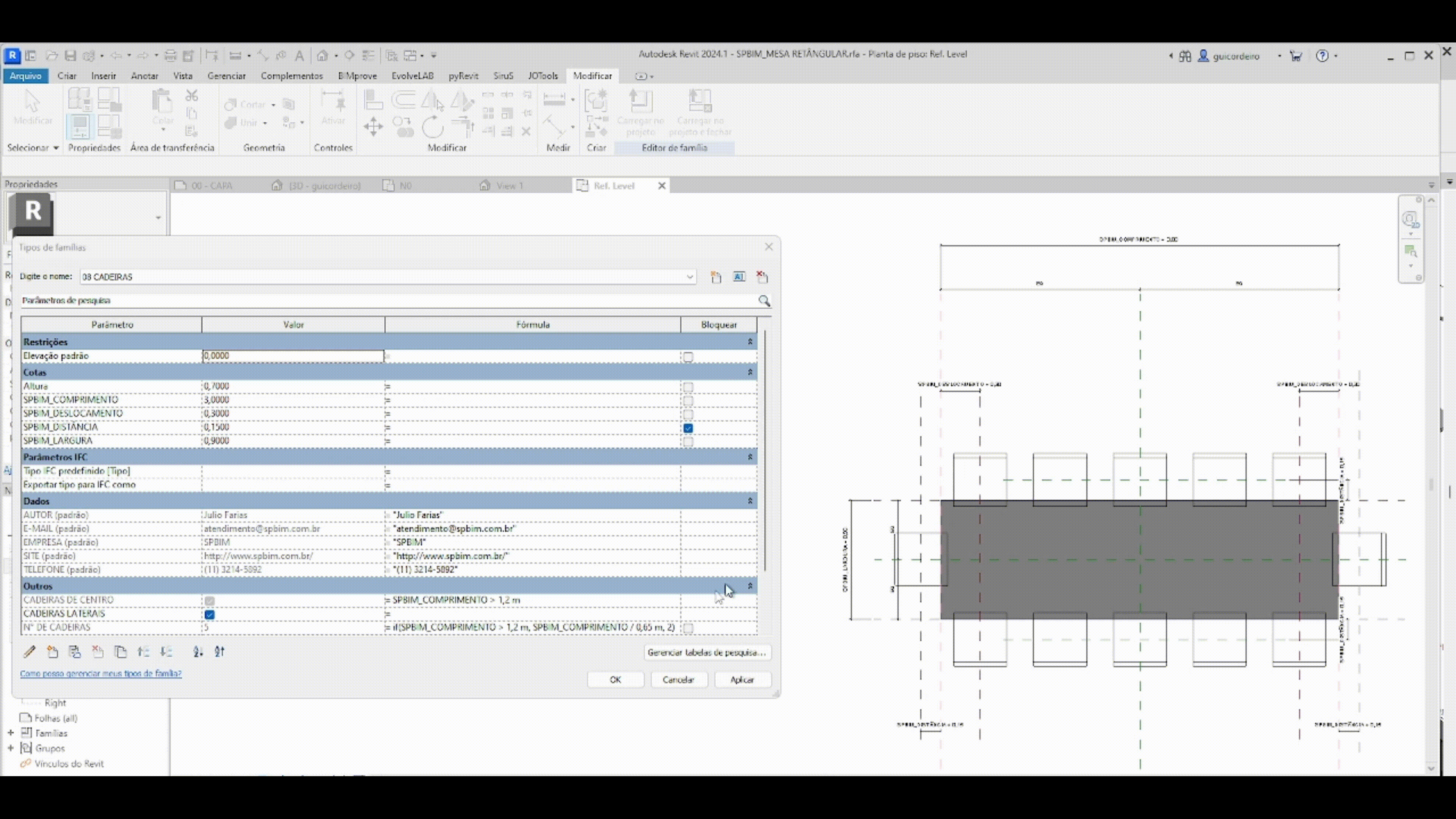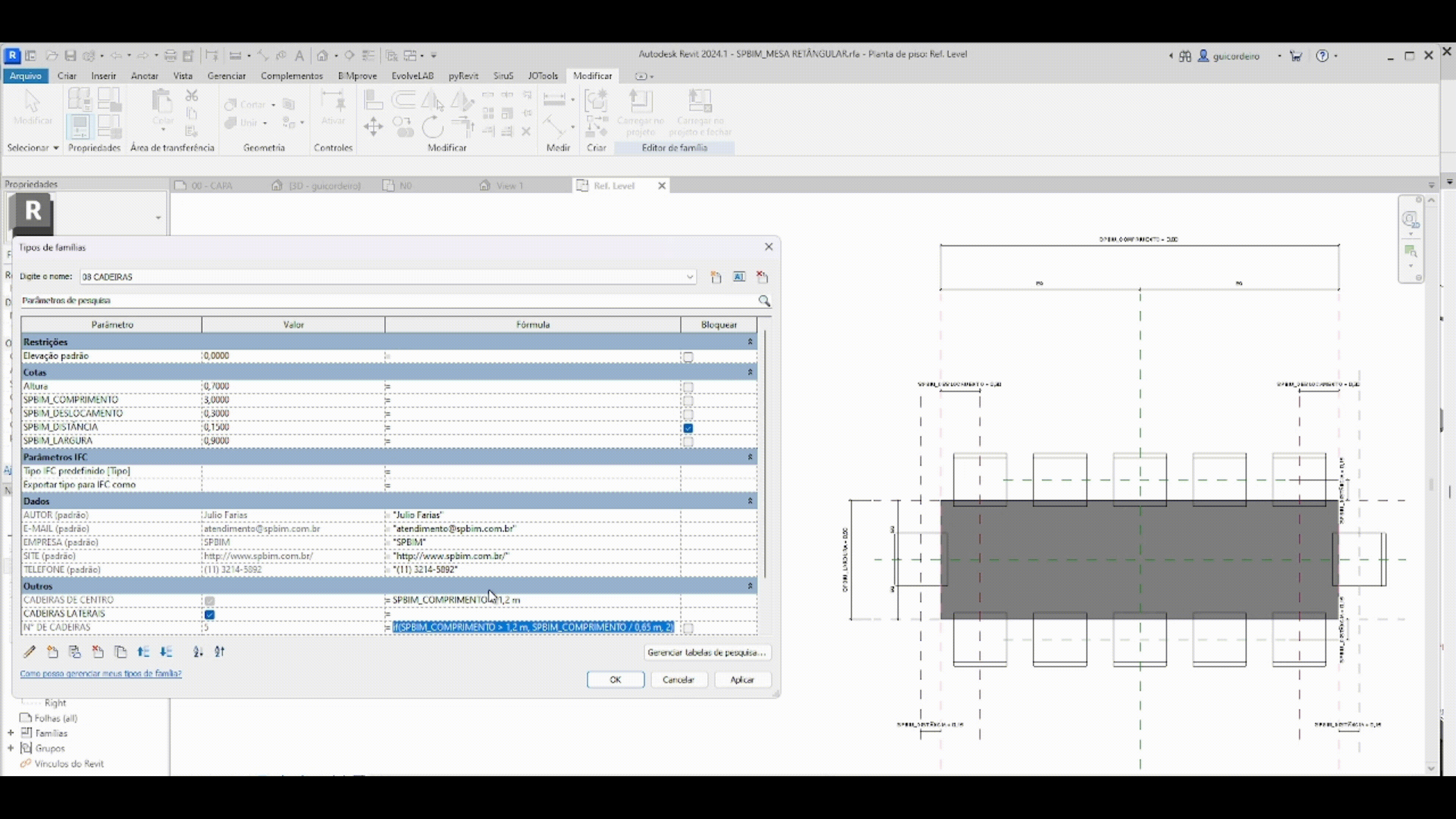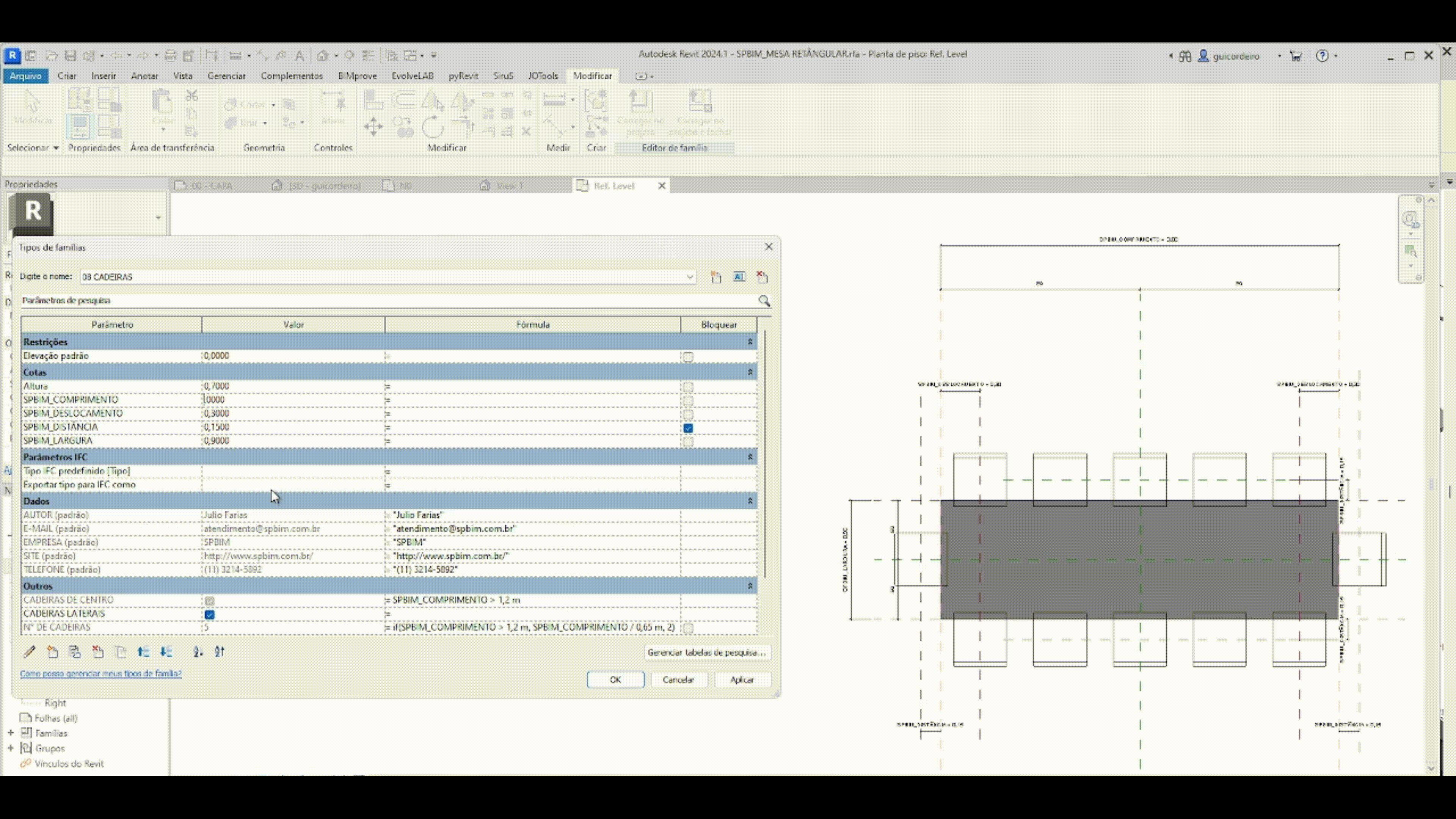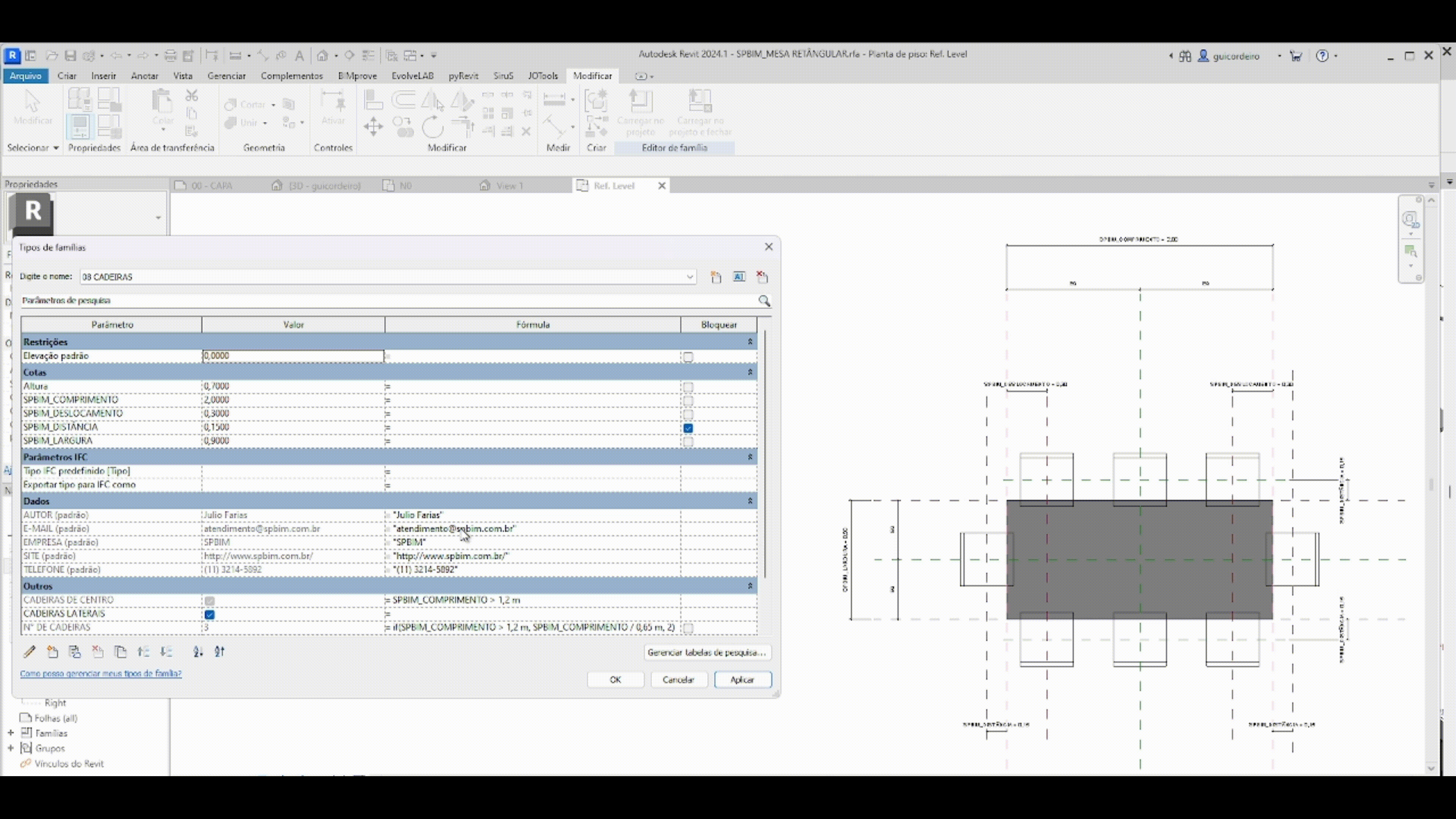
A fórmula condicional é a maneira de relacionar parâmetros e/ou valores que dependem de uma entrada específica, indicando uma saída para um resultado verdadeiro e/ou falso. A estrutura simples de uma declaração condicional está explicada na imagem abaixo.
Levando em consideração que em um projeto elétrico há inúmeras tomadas, otimizamos o tempo de posicionamento das mesmas aplicando a regra que as caixas de sobrepor com menos de duas tomadas, vão ter altura de 30 cm do chão, e as caixas de sobrepor com mais de duas tomadas, vão ter altura de 1,30 m do cão.
IF – Se, na hipótese de.
CONDIÇÃO – número de tomadas na caixa de sobrepor maiores que duas
VERDADEIRO – resultado caso tenha mais de duas tomadas na caixa
FALSO – resultado caso tenha menos de duas tomadas na caixa
FÓRMULA CONDICIONAL COM OPERADORES BOOLEANOS
A fórmula condicional com operadores booleanos também segue a proposta de relacionar parâmetros e/ou valores que dependem de uma entrada específica, indicando uma saída para um resultado verdadeiro e/ou falso, permitindo criar condições mais complexas em múltiplas situações. São eles: AND, OR e NOT (E, OU e NÃO).
Seguindo com a temática das tomadas de um projeto elétrico, quero classificar as tomadas em 110v e 220v com base na informação de largura e altura da caixa de sobrepor. Pensando que as caixas maiores que 11,5 cm de largura, 7 cm de altura são 220v, deste modo o parâmetro “220v” como sim se ambos, “largura” for maior que 11,5 e “altura” for maior que 7. Fugindo dessa regra “220v” deve ser “não”.
IF – Se, na hipótese de.
CONDIÇÃO 1 – “Largura > 11,5” – Verifica se o valor de largura é maior do que 11,5.
CONDIÇÃO 2 – “Altura > 7,0” – Verifica se o valor de altura é maior do que 7,0.
VERDADEIRO – “1” – Retorna o valor “1” sem ambos os valores forem verdadeiros, que representa “sim”
FALSO- “0” – Retorna o valor “0” sem um ou ambos os valores forem falsos, que representa “não”.
FUNÇÕES TRIGONOMÉTRICAS
Uma função trigonométrica é uma função matemática que relaciona os ângulos de um triângulo com as proporções entre seus lados. As principais funções trigonométricas são o seno, cosseno e tangente, é com elas que possibilita achar valores desconhecidos de um triângulo.


É fundamental destacar também as funções trigonométricas inversas (ou funções arcos), que permitem determinar os ângulos correspondentes a partir dos valores de seno, cosseno ou tangente, ademais é possível utilizar a raiz quadrada (sqrt) para a fórmula de pitágoras. Essas funções desempenham um papel crucial na resolução de problemas onde se conhece o valor dessas razões trigonométricas, mas se deseja calcular o ângulo associado.

ARREDONDAMENTO
O arredondamento de números é o processo de ajustar um número para um valor mais próximo, como a quantidade de casas decimais desejadas. Esse procedimento é amplamente utilizado para simplificar cálculos e apresentar resultados de maneira mais prática, evitando números muito longos ou complexos. O arredondamento pode seguir regras distintas, como arredondar para o número inteiro mais próximo, para cima (arredondamento para cima), ou para baixo (arredondamento para baixo). Neste contexto o revit usa do inglês, round, para abreviar arredondamento.

O Revit por sua vez não aplica arredondamento em ÁREAS e COMPRIMENTO de uma forma direta, é necessário o uso de fórmulas, são elas:
- ÁREAS: round(Area / 1 m²) X (1 m² / 1)
- COMPRIMENTO: round(Length / 1000 mm) * (1000 mm /1)
Dito isso, “1m² ” e “1000 mm” representam o decimal e são ajustáveis às necessidades.
PI (π)
O número π (pi) é uma constante matemática que representa a razão entre a circunferência de um círculo e seu diâmetro, sendo aproximadamente 3.14159265…. Ele é um número irracional, ou seja, tem infinitas casas decimais sem padrão de repetição, e também é transcendental, não podendo ser raiz de nenhuma equação polinomial com coeficientes inteiros.

LOGARITMOS E FUNÇÕES
Logaritmos são operações matemáticas que funcionam como o inverso da exponenciação. Por exemplo, no logaritmo de base 10 de 1000, a questão seria: “10 aumentou a qual potência resultado em 1000?” A resposta é 3, pois 10³ = 1000. O logaritmo é geralmente representado como log_b(x), onde “b” é a base e “x” é o número em questão.
O exponencial natural é uma função matemática definida como e^x, onde e é a constante de Euler, aproximadamente igual a 2,718. Essa função é fundamental no cálculo e aparece em diversos contextos, como no crescimento populacional, decaimento radioativo e modelagem de processos contínuos. Sua principal característica é que sua taxa de variação é sempre igual ao próprio valor da função, ou seja, a derivada de e^x é e^x, tornando-a essencial em equações diferenciais.
O logaritmo natural, denotado como ln(x), é a função logarítmica de base e, onde e é a constante de Euler (aproximadamente 2,718). Ele é definido como o inverso da função exponencial natural e^x, ou seja, ln(x) responde à pergunta: “A que potência devo elevar e para obter x?”. Essa função é amplamente utilizada em matemática, física e engenharia especialmente em modelagens de crescimento exponencial, decaimento, escalas logarítmicas e no cálculo de integrais e derivadas de funções exponenciais.
Já um valor absoluto de um número é sua distância até zero na reta numérica

BOAS PRÁTICAS PARA GARANTIR O FUNCIONAMENTO
Atenção às Unidades
- O Revit é sensível a unidades. Algumas operações podem exigir conversões.
- Se um parâmetro é de comprimento e outro é área, multiplicá-los pode gerar um erro.
- Para evitar problemas, use unidades coerentes ou crie parâmetros auxiliares.
Respeite a Ordem das Operações
O Revit segue a ordem matemática padrão:
- Parênteses: ()
- Potência: ^
- Multiplicação e divisão: * /
- Adição e subtração: + –
Exemplo:
(Largura + Altura) * 2
Se você escrever Largura + Altura * 2, o Revit multiplicará primeiro.
Verifique a Compatibilidade dos Parâmetros
- O Revit não permite misturar tipos de parâmetros diferentes (exemplo: comprimento com área).
- Se precisar converter um valor, crie um parâmetro intermediário.
Teste as Fórmulas Antes de Aplicá-las
- Insira valores simples para testar se o resultado está correto.
- Se a fórmula der erro, tente simplificá-la e testar por partes.
Use Parênteses para Evitar Ambiguidades
Sempre use parênteses para deixar claro o que deve ser calculado primeiro.
Exemplo:
(Largura + Altura) / 2
Evite Dependências Circulares
Se um parâmetro depende de outro que depende do primeiro, o Revit gerará erro.
Exemplo de erro:
A = B * 2
B = A / 2
Aqui, A e B dependem um do outro.
Utilize Parâmetros Compartilhados com Cuidado
Se estiver usando Parâmetros Compartilhados, garanta que eles estão bem configurados para evitar problemas na fórmula.
Nome dos parâmetros
Defina nomes para os parâmetros que não contenham números e/ou símbolos de operações para evitar erros de interpretação do software.
CONCLUSÃO
Há uma variedade imensa de possibilidades de parametria disponível para uso dentro do Revit e compreender seu funcionamento e condicionantes permite criar objetos e projetos de maneira mais eficiente, garantindo assertividade e mitigando erros humanos.












